Statistiek - Inleiding: verschil tussen versies
| Regel 3: | Regel 3: | ||
== Definitie == | == Definitie == | ||
| − | + | Wat statistiek voor mij zoal betekent: | |
| + | |||
| + | Statistiek beschrijft fenomenen die door toeval bepaald worden | ||
Statistiek houdt zich bezig met fenomenen die geen eenduidige | Statistiek houdt zich bezig met fenomenen die geen eenduidige | ||
status hebben. | status hebben. | ||
| − | + | Misschien wel de essentie van statistiek voor mij: Door studie van een steekproef kan ik uitspraken doen over de populatie als geheel. Da's echt heel koel: | |
| − | Statistiek houdt zich bezig met fenomenen die | + | Statistiek houdt zich bezig met fenomenen die door het toeval |
| − | + | bepaald worden, door analyse van een beperkt aantal instanties | |
van deze fenomenen. | van deze fenomenen. | ||
| − | + | Statistiek beschrijft fenomenen waarvan eigenschappen of | |
| + | gebeurtenissen door het toeval worden bepaald, door analyze van | ||
| + | een beperkt aantal instanties van deze fenomenen. | ||
| − | Statistiek | + | Statistiek voorspelt het gedrag van fenomenen waarvan eigen- |
| − | + | schappen of gebeurtenissen door het toeval worden bepaald, door | |
| − | + | analyze van een beperkt aantal instanties van deze fenomenen. | |
| − | + | Statistiek doet uitspraken over fenomenen die onderhevig zijn | |
| + | aan toeval, door analyse van een beperkt aantal instanties van | ||
| + | die fenomenen. | ||
| − | Voorbeeld: | + | Voorbeeld: Dankzij statistiek kun je iets zeggen over de populariteit van een politicus, door slechts een x-aantal mensen te ondervragen. |
== Populatie & steekproef == | == Populatie & steekproef == | ||
Versie van 2 apr 2018 14:41
Veel operationele beslissingen rondom online marketing, zoals bij advertentiecampagnes met Google AdWords of op Amazon, hebben te maken met statistiek. In het bijzonder: Wat is statistisch significant?. Zie artikel Statistiek & online marketing - Vuistregels voor practische hulp. Dit is een inleidend artikel.
Definitie
Wat statistiek voor mij zoal betekent:
Statistiek beschrijft fenomenen die door toeval bepaald worden
Statistiek houdt zich bezig met fenomenen die geen eenduidige status hebben.
Misschien wel de essentie van statistiek voor mij: Door studie van een steekproef kan ik uitspraken doen over de populatie als geheel. Da's echt heel koel:
Statistiek houdt zich bezig met fenomenen die door het toeval bepaald worden, door analyse van een beperkt aantal instanties van deze fenomenen.
Statistiek beschrijft fenomenen waarvan eigenschappen of gebeurtenissen door het toeval worden bepaald, door analyze van een beperkt aantal instanties van deze fenomenen.
Statistiek voorspelt het gedrag van fenomenen waarvan eigen- schappen of gebeurtenissen door het toeval worden bepaald, door analyze van een beperkt aantal instanties van deze fenomenen.
Statistiek doet uitspraken over fenomenen die onderhevig zijn aan toeval, door analyse van een beperkt aantal instanties van die fenomenen.
Voorbeeld: Dankzij statistiek kun je iets zeggen over de populariteit van een politicus, door slechts een x-aantal mensen te ondervragen.
Populatie & steekproef
Statistiek poogt iets te zeggen over een populatie van fenomenen door studie van een beperkte set van deze fenomenen, namelijk een steekproef
Fenomenen & experimenten
Statistiek houdt zich bezig met fenomenen. Dat zijn gebeurtenissen of eigenschappen die (binnen de gegeven context) onderhevig zijn aan toeval. Voorbeelden:
- Tossen met een munt - Wordt kop gegooid?
- Gooien met een dobbelsteen - Welk getal wordt gegooid?
- Alle sterren in de melkweg - Wat is de temperatuur?
- Alle sterren in het universum - Wat is de temperatuur?
- Een AdWords-campagne - Wordt er op een advertentie geklikt?
- Een bezoeker op een site dankzij een AdWords-campagne - Converteert deze bezoeker?
In deze voorbeelden werd steeds gesproken over losse gebeurtenissen. Dat hoeft niet altijd zo te zijn - Pas op voor verwarring.
Vaak spreekt men hier van experimenten, trials, evenementen, testen, etc.
Toeval, causualiteit & modelvorming
Men spreekt van toeval als de betreffende gebeurtenis of eigenschap niet te verklaren is aan de hand van een oorzaak. Dus een gebeurtenis zonder aanwijsbaar causaal verband.
Vaak zal dit een kwestie van context zijn: Als ik bezoekersgedrag rondom een AdWords-campagne analyseer, is er wel degelijk een causaal verband waarom een bepaalde bezoeker een bepaalde actie doet, maar die informatie heb ik niet. Dit valt dus buiten de context: In de gegeven situatie is er geen informatie omtrent die causaliteit. Het fenomeen kan dus beschouwd worden als zijnde zonder aanwijzbare oorzaak.
Nu wordt het interessant: Door statistische analyse kan ik wel degelijk iets zeggen over de achterliggende causualiteit. Door bv. te split-testen kan ik achterhalen dat landing page A beter bevalt dan landing page B. Alsof ik hiermee de toeval enigszinds terugdring en de causualiteit in het gedrag van de bezoekers laat toenemen.
Een andere manier om dit te formuleren: Mede dankzij statistiek ontwikkel ik een model dat steeds accurater het gedrag van bezoekers beschrijft, en dat steeds minder gebaseerd is op ruwe geaggregeerde statistiek.
Stochastische variabele
De kern van een fenomeen-met-toeval, is wellicht de stochastische variabele of stochastische grootheid
Voorbeeld - Tossen
Beschouw het opgooien van een munt:
- Dit betreft een experiment met twee mogelijke uitkomsten
- Uitkomst kop beschouwen we als een sucess (1). Uitkomst munt (0) beschouwen we als een mislukking
- Twee uitkomsten + success/mislukking? ⇒ Dit is een Bernoulli trial, binomial trial, Bernoulli-verdeling of binomiaal-verdeling [1]
De bijbehorende kansfunctie:
- px(1) = P(X=1) = p
- px(2) = P(X=0) = 1-p
Hierbij is p de kans op succes. Alternatieve notering:
- f(k;p)=
- p als k=1
- 1-p als k=0
Verwachtingswaarde:
- E(X)=p*(1) + (1-p)*(0)
Voor een zuivere munt is deze:
- E(X) = (1/2)*1 + (1/2)*=0 = 1/2
Variantie:
- var(X) = p(1-p) = (1/2)(1-(1/2) = 1/4
Het gemiddelde van een reeks steekproeven, wordt aangeduid met x̄ of μ [2][3]
Voorbeeld: Dobbelen
Beschouw het gooien met een zuivere dobbelsteen. Hierbij geldt:
- x - Discrete stochastische variabele
- Populatie of waardebereik van x is gegen door {1,2,3,4,5,6}
- p(x) - Kansfunctie
- P(X) - Gerealiseerde kans op een gegeven uitkomst.
De kansfunctie px of px(x) is hierbij gegeven door:
- px(1) = P(X=1) = 1/6
- px(2) = P(X=2) = 1/6
- px(3) = P(X=3) = 1/6
- px(4) = P(X=4) = 1/6
- px(5) = P(X=5) = 1/6
- px(6) = P(X=6) = 1/6.
Merk op dat een kansfunctie zoals px anders is dan een gewone wiskundige functie, omdat bij kansfuncties niet sprake is van een bepaalde input. Daarnaast is de 'output' een kans dat de input had kunnen optreden, en niet een bewerking op de input.
De verwachtingswaarde is in dit geval de sommatie van alle uitkomsten * kan, en is hier:
- E(X) = sigma_overx x * px(x)
- = 1*P(X=1) + 2*P(X=2) + ... + 6*P(X=6) = 3,5
Een gooi met de dobbelsteen vormt een steekproef, monster, observatie, staal, sample of trial.
Het probleem: 100 steekproeven zonder success. Wat nu?
De verwachtingswaarde gaat uit van een oneindig aantal steekproeven, maar in de praktijk is het aantal trials beperkt. Wellicht is dit de fantastische wereld van utiliteitswaarde, expected value of sample information, etc.
Simpel AdWords-voorbeeld
- Een conversie is € 20 waard
- Een klik kost € 1
- 100 Klikken op rij hebben geen conversie opgeleverd
- Kosten van de trials: € 100. Opbrengst: € 0. Resultaat: € -100
- P(X=0) = 100%
- P(X=1) = 0%
- De verwachtingswaarde van deze kansfunctie is 0.
- Als er geen rekening wordt gehouden met het eindige aantal trials, is de conclusie simpel: Stoppen.
Conversie op de 101e trial
Maar nu vindt er een conversie plaats op de 101e trial. Nieuwe gegevens:
- 101 Klikken op rij
- Kosten: € 101
- Verwachtingswaarde: 1/101 * € 20 = 0,01 * € 20 = € 0,20
- P(X=0) = 99%
- P(X=1) = 1%
- Kosten: € 101. Opbrengst: € 20. Resultaat: € -81
Conclusies tav. dit voorbeeld
- Deze ene conversie heeft niet de campagne gered. Het was waarschijnlijk niet de moeite waard om deze additionele trial te doen
- In de praktijk is het wijsheid om (bij afwezigheid van additionele gegevens) een campagne te pauzeren als er 100 trials zijn geweest zonder ook maar één conversie, en waarbij een komende conversie niet in één keer de campagne redt
- Voor een degelijker antwoord moet je met zekerheidsintervallen aan de slag.
Variantie
- Variantie is een maat van de spreiding van de uitkomsten van een experiment
- Het is een maat van de onderlinge afwijking tussen uitkomsten of waarden
- Het is een maat voor de afwijkingen tav. de gemiddelde uitkomst
- Min-of-meer: Gemiddelde van het kwadraat van de afwijkingen
- Tav. waarden van een populatie, spreekt men van populatievariantie, σ2
- Tav. uitkomsten van een steekproef, spreekt met van steekproefvariantie, s2
- Tav. waarden van een verdeling, spreekt met gewoon van variantie
- De wortel van de steekproefvariantie, is de standaardafwijking σ (sigma).
De formule ziet er vaak heftiger uit dan-ie is:
- σ^2 = (1/N) sommatie (i=1 → N) (xi-μ)2
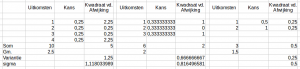
Voorbeeld: Kop of munt (1)
- Observaties: {1,0,0,1,1}
- N=5
- μ = 3/5 = 0,6
Variantie:
- σ2 = (1/5) * {(1-0,6)2 + (0-0,6)2 + (0-0,6)2 + (1-0,6)2 + (1-0,6)2} <=>
- σ2 = (1/5) * {0,16 + 0,36 + 0,36 + 0,16 + 0,16)} <=>
- σ2 = (1/5) * {1,2} <=>
- σ2 = 0,24.
Voorbeeld: Kop of munt (2)
Voor een oneindige reeks (N → ∞) met een zuivere munt krijg je:
- σ2 = (1/2) * {(1-1/2)2 + (0-1/2)2} <=>
- σ2 = (1/2) * {(1/2)2 + (1/2)2} <=>
- σ2 = 1/4
Intuïtief: Er zijn twee mogelijke uitkomsten. Die wijken allebei een 1/2 af van het gemiddelde. Het kwadraat hiervan is 1/4.
Voorbeeld: Zuivere dobbelsteen
Standaarddeviatie
Van variantie naar standaarddeviatie
- Standaarddeviatie of standaardafwijking is de wortel van de variantie, aangeduid met :σ
- Vaak is het handig om de standaarddeviatie te gebruiken ipv. de variantie, omdat deze van dezelfde ordergrootte is, als die van de uitkomsten van het betreffende experiment
- Let op: Je kunt de standaardeviatie niet berekenen door in de formule voor de variantie links en rechts machtsverheffen weg te laten (omdat er tussentijds wordt opgeteld).
Spreiding
- Met spreiding wordt losjes bedoeld, de verschillen tussen de waarden die een stochastische variabele vertoont
- Op het moment dat met een spreiding een kwantitatieve grootheid wordt bedoeld, gaat het meestal om de standaardafwijking of standaarddeviatie.
Maat voor de spreiding
Hypothese
Na de practische hoofdstukken hiervoor, nu weer terug naar de theorie, te beginnen met de begrippen toetsingstheorie en hypothese.
De reden om statistiek te bedrijven binnen online adverteren, is vanwege statistische toetsingstheorie: We hebben een bepaalde theorie, en die willen we statistisch toetsen. Hierbij wordt uitgegaan van één of meer hypothesen of veronderstellingen ten aanzien van een onderliggende kansverdeling. Qua hypothesen maken we daarbij onderscheid tussen de nulhypothese H0 en de alternatieve hypothese H1 of HA. De nulhypothese gaat ervan uit dat het vermoede verband of effect niet bestaat. HA gaat er van uit dat het gezochte effect wél bestaat. Met behulp van statistische toetsing proberen we theorie HA te bewijzen.
Voorbeeld: Verkoudheid bij mannen en vrouwen
- Theorie: Vrouwen zijn vaker verkouden dan mannen
- H0: Vrouwen zijn niet vaker verkouden dan mannen
- HA: Vrouwen zijn vaker verkouden dan mannen
Toetsing:
- Een steekproef wordt genomen van 1.000 willekeurige mannen en 1.000 willekeurige vrouwen. Hen wordt gevraagd hoe vaak zij het afgelopen jaar verkouden waren.
- Naarmate het aantal vrouwen dat vaker verkouden was dan mannen stijgt, wordt de nulhypothese minder aannemelijk. Uiteindelijk wordt de nulhypothese verworpen
- De kans dat de nulhypothese ten onrechte wordt verworden, is de onbetrouwbaarheid \alpha van de toets
- Het kan gebeuren dat de nulhypothese niet wordt verworpen, terwijl er wel degelijk een effectie is. De kans hierop wordt het onderscheidend vermogen \gamma genoemd
- Om iets zinnigs te zeggen over \alpha en \gamma, is het oa. nodig iets te weten over de onderliggende kansverdeling.
Statistische toets - Voorbeeld gewogen dobbelsteen
Een dobbelaar vermoedt dat de '6' minder vaak valt dan te verwachten:
- De kans dat de '6' valt, wordt aangeduid met p
- H0: p=1/6 - Dobbelsteen is eerlijk
- H1: p<1/6 - Kans dat de '6' valt, is minder dan 1/6
Toetsing middels 600 steekproeven en verschillende scenario's:
- Als de '6' 100 keer valt → H0 bevestigd
- Als de '6' 98 of 99 keer valt → H0 bevestigd
- Als de '6' slechts 0 of 1 keer valt → H0 verworpen
'6' Valt 80 keer
Nu wordt het interessanter: De '6' valt 80 keer. Wat nu?
- Bij een eerlijke dobbelsteen, is de kans hierop slechts 1% (kun je zelf uitrekenen, schijnt)
- Hypothese H0 kan met 99% zekerheid verworpen worden
- Er is echter een kans van 1% dat H0 ten onrechte verworpen wordt: Fout van de eerste soort
- Dus de onbetrouwbaarheid van de toetsing is hier 1%
Als max. 0,1% onbetrouwbaarheid wordt vereist?
- Dan wordt H0 pas verworpen als de '6' 72 keer of minder valt
Als max. 0,5% onbetrouwbaarheid wordt vereist?
- Dat komt overeen met een zekerheidsinterval van 99,5%
- Dan wordt H0 verworpen als de '6' 84 keer of minder valt.
Als de '6' in werkelijkheid 1/8 keer valt?
- Dan zou bij 600 steekproeven, de '6' naar verwachting 88 keer vallen ipv. 100 keer
- Naarmate de betrouwbaarheid minder belangrijk is, zal dit sneller gedetecteerd worden, maar wél met een grotere onzekerheid
- Bij een 99% zekerheidsinterval, is 80 al significant → Afwijking wordt gedetecteerd
- Bij een 99,9% zekerheidsinterval, is 72 pas een significant aantal → Afwijking wordt niet gedetecteerd
- Bij een 99,5% zekerheidsinterval, is 84 pas een significant getal → Afwijking wordt niet gedetecteerd
- Dit getal van 88%, heet het onderscheidend vermogen voor deze situatie.
Dit voorbeeld geformaliseerd
Probleemstelling
De probleemstelling behelst de verdeling en de steekproef:
- 600 Worpen met een dobbelsteen
- Aantal keer dat '6' wordt gegooid, noemen we X
- Stochastische variabele X is B(600,p)-verdeeld, met onbekende parameter p
Hypothesen
- H0: p = 1/6
- H1: p < 1/6
Toetsingsgrootheid
Als toetsingsgrootheid nemen we:
- T = X
Verdeling onder de nulhypothese
- Onder H0 is T binomiaal verdeeld met parameters n=600 en succeskans 1/6
- Omdat n zo groot is, kan deze verdeling beschouwd worden als een normale, met verwachting np=100 en variantie np(1-p)=83,33 en standaardafwijking = sqrt(83,33) = 9,13.
Steekproefuitkomst
Waarde t die de toetsingsgrootheid aanneemt bij de steekproefuitkomst:
- Er wordt 80 keer 6 gegooid. Dus voor X wordt de waarde x=80 gevonden
- Waargenomen waarde t is dus: T=t=80.
Kritieke gebied
We verwerpen de nulhypothese voor kleine waarden van T, zeg voor T ≤ c. De kritieke waarde c volgt uit:
- P(fout type I)=supH0P(verwerp H0) = supH0 P(T =< c) =< alpha0,
waarin \alpha0 de vooraf gekozen onbetrouwbaarheidsdrempel is. Voor bijvoorbeeld \alpha_0=5% wordt dit:
- 0,05 >= supH0 P(T =< c) = P(Z=<(c-100)/9,13)
Waarin Z de zogenaamde Z-score is, de onder de nulhypothese gestandaardiseerde toetsingsgrootheid. Omdat voor grote steekproefomvang T ,en dus ook Z, bij benadering normaal verdeeld is, en \phi(1{,}65) = 0{,}95, volgt
- c=100 - 9,13 x 1,65 = 85,0
Zie ook Overschrijdingskans.
Conclusie
De gevonden waarde t=80 ligt in het kritieke gebied, dus we verwerpen de nulhypothese. Of, alternatief: de overschrijdingskans is 0,014, dus veel kleiner dan de onbetrouwbaarheidsdrempel 0,05; we verwerpen de nulhypothese.
Bronnen
Algemeen
- https://nl.wikipedia.org/wiki/Statistiek
- https://www.youtube.com/watch?v=09kiX3p5Vek - Standard deviation
- https://nl.wikipedia.org/wiki/Categorie:Statistiek
- http://nl.wikipedia.org/wiki/Verwachting_%28wiskunde%29
- http://en.wikipedia.org/wiki/Expected_value_of_sample_information
- http://en.wikipedia.org/wiki/Confidence_interval
- http://nl.wikipedia.org/wiki/Betrouwbaarheidsinterval
- http://nl.wikipedia.org/wiki/Binomiale_verdeling
- http://nl.wikipedia.org/wiki/Verwachte_nutshypothese
- http://en.wikipedia.org/wiki/Expected_utility_hypothesis
- http://en.wikipedia.org/wiki/Statistical_inference
- http://en.wikipedia.org/wiki/Standard_deviation
- http://en.wikipedia.org/wiki/Variance
- http://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
- https://en.wikipedia.org/wiki/Null_hypothesis
- https://nl.wikipedia.org/wiki/Hypothese_%28statistiek%29
- https://nl.wikipedia.org/wiki/Statistische_toets
- http://www.hhofstede.nl/modules/normaal.htm
- https://en.wikipedia.org/wiki/Bernoulli_trial
- https://hbr.org/2016/02/a-refresher-on-statistical-significance
- http://www.personal.psu.edu/ejp10/blogs/gotunicode/2010/03/dealing-with-x-bar-x-and-p-hat.html
Statistiek & AdWords
- http://www.chadsummerhill.com/ppc-text-ad-test-statistical-validity/
- http://www.chadsummerhill.com/statistically-significant-ppc-testing-google-math/
- http://www.marketingexperiments.com/blog/practical-application/top-14-free-marketing-tools-and-resources.html
- http://www.marketingexperiments.com/images/multifiles/Data-Sample-Statistically-Valid.pdf
- http://adalysis.com/blog/working-with-statistical-significance-how-confident-should-you-be-in-your-test-results/
- http://adalysis.com/blog/how-much-data-should-you-have-before-examining-an-ad-test-result
- http://adalysis.com/blog/do-you-have-insignificant-test-results-how-to-use-maximum-data-in-ad-testing/